Uma equação quadrática é feita a partir de um termo latino "quadrados", que significa quadrado. É um tipo especial de equação com no formato:

  ax²+bx+c=0

  Aqui, "x" é desconhecido que você deve encontrar e "a", "b", "c" especifica os números de forma que "a" não seja igual a 0. Se a = 0, a equação torna-se linear e não mais quadrática .

  Na equação, a, b e c são chamados de coeficientes.

  Vejamos um exemplo para resolver a equação de segundo grau: 8x² + 16x + 8 = 0.

  Arquivo: 67-funcaoQuadratica.py:

   # Como Resolver uma Equação Quadrática. # Importar o módulo complexo math, import cmath a = float(input('Informe o valor de a: ')) b = float(input('Informe o valor de b: ')) c = float(input('Informe o valor de c: ')) # Calcular o discriminante. d = (b**2) - (4*a*c) # Encontra duas soluções. sol1 = (-b-cmath.sqrt(d))/(2*a) sol2 = (-b+cmath.sqrt(d))/(2*a) print('As soluções são: {0} e {1}'.format(sol1,sol2))

  Para compilar o código, utilize qualquer compilador de sua preferência ou utilize o compilador online abaixo:

  Compilador Online Python

  Veja na imagem abaixo o resultado desse código:

  Explicação do código:

  Na primeira linha, importamos o módulo cmath e definimos três variáveis denominadas a, b e c, que recebem informações do usuário. Em seguida, calculamos o discriminante usando a fórmula. Usando o método cmath.sqrt(), calculamos duas soluções e imprimimos o resultado.

  Segundo método:

  Podemos obter a solução da equação quádrica usando a fórmula direta. Vamos entender o seguinte exemplo.

  A fórmula acima consiste nos seguintes casos:

  1) Se b2 < 4ac, então as raízes são complexas (não reais). Por exemplo - x2 + x + 1, as raízes são -0,5 + i1,73205 e +0,5 - i1,73205.
  2) Se b2 == 4ac, então ambas as raízes são iguais Por exemplo - x2 + x + 1, as raízes são -0,5 + i1,73205 e +0,5 - i1,73205.
  3) Se b2 > 4ac, então as raízes são reais e diferentes. Por exemplo - x2 - 7 x - 12, as raízes são 3 e 4.

  Vejamos um exemplo.

  Arquivo: 67-funcaoQuadratica-2.py:

   # Como Resolver uma Equação Quadrática. # Segundo Método. import math # Função para encontrar a raiz. def findRoots(a, b, c): dis_form = b * b - 4 * a * c sqrt_val = math.sqrt(abs(dis_form)) if dis_form > 0: print(" raízes reais e diferentes ") print((-b + sqrt_val) / (2 * a)) print((-b - sqrt_val) / (2 * a)) elif dis_form == 0: print(" raízes reais e iguais") print(-b / (2 * a)) else: print("Raízes Complexas:") print(- b / (2 * a), " + i", sqrt_val) print(- b / (2 * a), " - i", sqrt_val) a = int(input('Informe o valor de a: ')) b = int(input('Informe o valor de b: ')) c = int(input('Informe o valor de c: ')) # Se a for 0, entao a equaçao está incorreta. if a == 0: print("Insira a equação quadrática correta:") else: findRoots(a, b, c)

  Veja na imagem abaixo o resultado desse código:

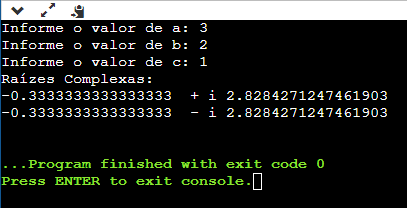
  Explicação do código:

  Na primeira linha, importamos o módulo cmath e definimos três variáveis denominadas a, b e c, que recebem informações do usuário. Em seguida, calculamos o discriminante usando a fórmula. Usando o método cmath.sqrt(), calculamos duas soluções e imprimimos o resultado.